霍尔系数的物理意义是什么（从霍尔效应到量子霍尔效应）

电子是构成物质的基本粒子之一，它们在导体或半导体中自由地运动，形成电流。但是当我们把这些电子限制在二维空间中，并施加一个垂直于平面的强磁场时，它们会展现出一些令人惊讶和迷人的行为。这就是量子霍尔效应，一种霍尔效应的量子力学版本。

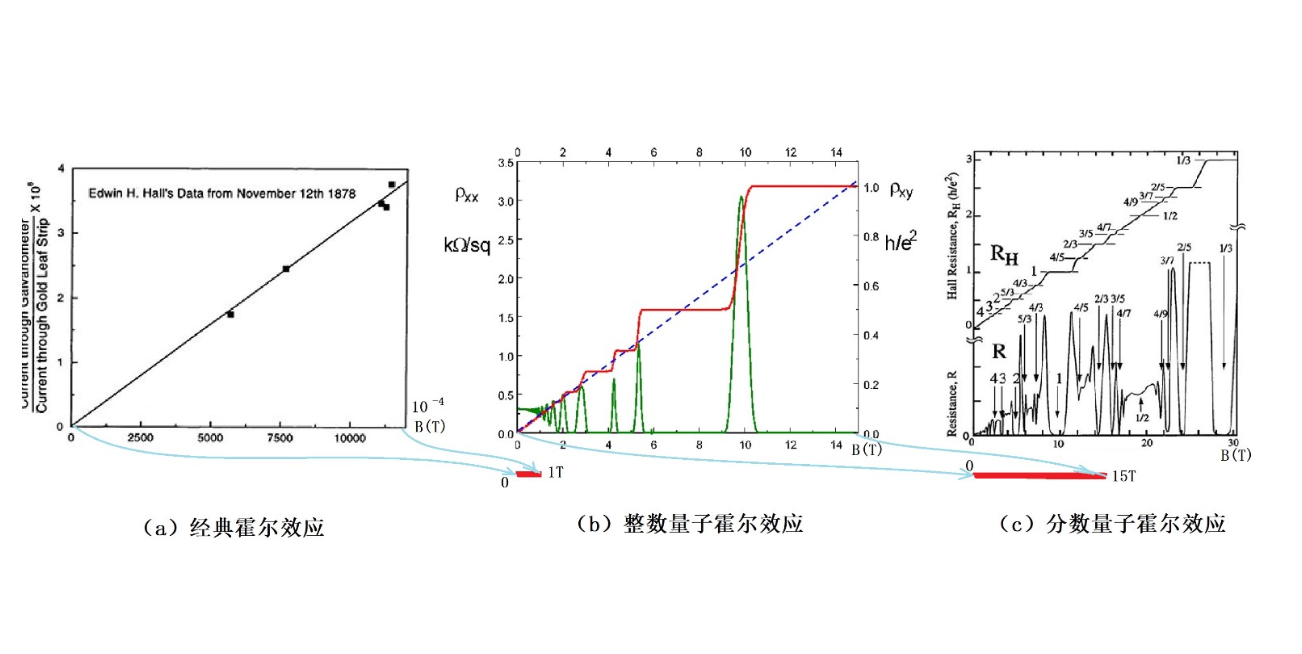
霍尔效应是在1879年由美国物理学家霍尔发现的。他发现，在一个有电流通过的导体中，如果沿垂直于电流方向施加一个磁场，那么在垂直于电流和磁场方向上会产生一个横向电压，称为霍尔电压。这个电压与电流和磁场成正比，其比例系数称为霍尔系数。霍尔效应可以用来测量导体或半导体中载流子（电子或空穴）的类型和密度。

然而，在20世纪80年代初，德国物理学家冯·克利青在法国格勒诺勃的强磁场实验室做了一个惊人的发现。他用一种特殊的器件，叫做金属-氧化物半导体场效应晶体管制造了一个二维电子气系统。他在极低温和强磁场下测量了这个系统的霍尔电阻（霍尔电压与电流之比）。他发现，霍尔电阻并不随着磁场强度连续变化，而是出现了一系列平台，每个平台对应一个整数倍的普朗克常数除以电子电荷平方，这就是整数量子霍尔效应它表明了二维电子气系统中存在着能级量子化和无耗散输运的现象。冯·克利青因此获得了1985年诺贝尔物理学奖。

量子霍尔效应的物理机制是什么呢？为了解释这个问题，我们需要引入两个重要的概念：朗道能级和边缘态。

朗道能级是指在强磁场中的电子的量子化能级。按照经典电磁理论，处于强磁场中的电子会受到洛伦兹力的作用，而做圆周运动，形成回旋轨道。但是在量子力学中，这些回旋轨道是量子化的，每个轨道只能容纳有限数量的电子，称为朗道能级。朗道能级的能量与磁场强度成正比，而与电子密度无关。当磁场很强时，每个朗道能级可以容纳很多电子，而且所有的电子几乎都集中在最低的几个朗道能级上。这时，如果改变磁场强度或电子密度，就会导致朗道能级被填充或清空，从而使霍尔电阻出现量子化平台。

边缘态是指在样品边缘的电子的运动状态。由于外加磁场的作用，样品中间的电子被局域化在原地打转，不能参与电流输运。但是在样品边缘的电子，由于受到边缘的反弹作用，会沿着样品边缘从一端运动到另一端，形成一种单向的无散射的运动状态，称为边缘态。边缘态的存在使得二维电子气系统具有无耗散输运的特性，即当霍尔电阻处于某一平台值时，纵向电阻等于零。

量子霍尔效应不仅揭示了二维电子气系统中一些奇妙的物理现象，也为科学家们提供了一个探索新领域和新概念的平台。例如，在1982年，美国华裔物理学家崔琦和德国物理学家施特默在美国贝尔实验室发现了分数量子霍尔效应。这一发现表明了二维电子气系统中存在着一种强关联效应，即电子之间的库仑相互作用导致了一些新奇的准粒子（如涡旋和复合费米子）和分数统计（即不遵循玻色-爱因斯坦统计或费米-狄拉克统计）。崔琦因此与美国物理学家劳克林和施特默共同获得了1998年诺贝尔物理学奖。

量子霍尔效应还与拓扑不变量有着密切的联系。拓扑不变量是指一些不随系统参数连续变化而改变的整数或分数值，它们可以用来描述系统的拓扑性质和相变。例如，在整数量子霍尔效应中，填充因子f就是一个拓扑不变量，它可以用陈数或贝利曲率来表示；在分数量子霍尔效应中，则存在一些非阿贝尔的拓扑不变量，它们与准粒子的分数统计和任意性有关。拓扑不变量的概念在物理学中有着广泛的应用，它们可以用来刻画一些新奇的物态，如拓扑绝缘体、拓扑超导体、拓扑相变等。

量子霍尔效应是一个充满了奥秘和魅力的物理现象，它让我们看到了电子在极端条件下的非凡表现，也让我们认识了一些新的物理概念和数学工具，如朗道能级、边缘态、分数统计、拓扑不变量等。它还为我们提供了一个探索新领域和新物态的平台，如拓扑绝缘体、拓扑超导体、拓扑量子计算等。

量子霍尔效应不仅是一种基础的科学现象，也是一种有着重要应用价值的技术标准，它可以用来定义电阻单位和测量精细结构常数。量子霍尔效应是20世纪以来凝聚态物理领域最重要的科学发现之一，它为我们打开了电子世界的神秘面纱，也为我们展示了物理学的无穷魅力。